Geoprocessamento

Esse guia apresenta as etapas para o ajuste de modelos geoestatísticos multivariados utilizando o pacote {d2h}. É importante que o usuário tenha passado pelo guia introdutório antes seguir com esse guia.

1. Carregando um objeto `Inv`

Assim como todas as demais operações do pacote {d2h}, o modelo geoestatístico do pacote é construído em cima de um objeto da classe Inv. Nesse exemplo vamos carregar um arquivo shapefile

library(d2h)
#> 
#> Attaching package: 'd2h'
#> The following object is masked from 'package:stats':
#> 
#>     confint

caminho <- system.file('extdata', 'parcelas.shp',  package = 'd2h')

inv <- read.inv(path = caminho,   # Caminho até o arquivo
                variavel = 'va',  # "va" é o nome da coluna da variável de interesse
                par = 'parcela'   # "parcela" é o nome da coluna das parcelas
                )
#> ---------------------------------------
#> Nem todas as feições são polígonos: [POINT].
#> Área das parcelas deve ser informada via `areapar=`
#> ---------------------------------------

# Aparentemente tudo certo
inv
#>   Número de parcelas:  46 
#>    Área da parcela:  0  ha
#>    Área amostrada:  0  ha
#>    Fração amostral:  0 
#>  ------------------------------------------
#>    Área Total:  Inf  ha
#>    Método de Amostragem:  fixo 
#>    Processo de Amostragem:  Amostragem Aleatória Simples 
#>  ------------------------------------------
#>   Volume médio(a): 132.07 m³/ha
#>   Desvio Padrão(a): 25.53 m³/ha
#>  ------------------------------------------
#>   *Assumindo volume dado(a) em m³/ha.

plot(inv)

Para modelagem espacial, é obrigatório que exista o componente espacial do objeto Inv.

2. Modelagem espacial

A modelagem espacial é feita com os seguintes passos:

Ajuste do modelo
1. Definições do modelo
  1. Estrutura de covariância
  2. Função de autocorrelação
  3. Demais definições
2. valores iniciais dos parâmetros (opcional)
Predição (krigagem)
1. Definições de krigagem
2. Área e densidade de predição

2.1 Ajuste do modelo

O modelo geoestatístico é feito utilizando a função fit.geomodel(), e recebe como argumentos obrigatórios InvObj= e var_names=. O primeiro é o objeto Inv criado, e o segundo é um vetor contendo os nomes das variáveis que se deseja ajustar. O principal destaque da função é a possibilidade de ajuste de modelos multivariados ao passar mais de uma variável para var_names=.


minv <- fit.geomodel(InvObj = inv,              # Objeto `Inv`
                     var_names = c('va',  'h'), # Serão ajustadas "va" e "h"
                     )
#> ---------------------------------------------
#> Ajustado utilizando máxima verossimilhança.
#> Use ... (control) para passar argumentos adicionais a optim().
#> ATENÇÁO! O ajuste pode levar alguns minutos!
#> ---------------------------------------------
#> Estrutura de Covariância adotada: simpler
#> Ajuste em escala irrestrita (log/atanh conforme o caso).
#> ---------------------------------------------
#> Ajustando...
#> ---------------------------------------------
#> Fim da maximização numérica.
#> ---------------------------------------------
#> Tempo de otimização: 0.65 segundos
#> ---------------------------------------------

O resultado do ajuste é um objeto da classe GeoModel, que ao ser chamado apresenta algumas informações sobre o ajuste.


# Printar o modelo na no console resulta na apresentação dos parâmetros estimados
minv
#> --------------------------------------
#>            Modelo ajustado            
#> --------------------------------------
#> Estrutura de Covariância: Simpler (Dados co-locados)
#> --------------------------------------
#> Parâmetros marginais:
#>          mu   sigmas     phis   taus
#> va 130.7685 630.7728  60.7584 0.0602
#> h   24.4500   0.5443 314.1510 0.5624
#> --------------------------------------
#> Matriz de correlação:
#>           va         h
#> va 1.0000000 0.7068323
#> h  0.7068323 1.0000000
#> --------------------------------------
#> Ajuste realizado na escala irrestrita (log/atanh) dos parâmetros.
#> --------------------------------------
#> Log-verossimilhança maximizada: -262.4712

O método summary() apresenta o resumo estatístico do ajuste, tal qual com objetos gerados via lm().

summary(minv)
#> ------------------------------------------------------------
#> GeoModel — resumo do ajuste
#> Modelo: exponential | Cov estrutura: simpler
#> Estimado em escala irrestrita; EPs via delta method.
#> Convergência optim: 0
#> LogLik: -262.4712 | nobs: 92 | k: 9 | AIC: 542.9423 | BIC: 565.6384 
#> ------------------------------------------------------------
#>           Estimate Std. Error z value Pr(>|z|)
#> sigma[va] 630.8    132.4      4.766       0   
#> sigma[h]  0.5443   0.3049     1.785   0.0743  
#> phi[va]   60.76    32.62      1.863   0.0625  
#> phi[h]    314.2    218.9      1.435   0.1512  
#> mu[va]    130.8    3.907      33.47       0   
#> mu[h]     24.45    0.2947     82.95       0   
#> tau[va]   0.0602   12.74      0.0047  0.9962  
#> tau[h]    0.5624   0.275      2.045   0.0409  
#> rho[va×h] 0.7068   0.0755     9.361       0   
#> ------------------------------------------------------------
#> Nota: parâmetros > 0 testados ao redor de 0 na escala final.

A seguir serão apresentadas as definições gerais do modelo, e alguns dos próximos argumentos de fit.geomodel().

2.1.1 Definições do modelo

2.1.1.1 Estrutura de covariância

Os modelos geoestatísticos implementados no pacote {d2h} são modelos gaussianos multivariados, com a possibilidade de escolha de diferentes estruturas de covariância. Atualmente estão implantadas duas estruturas: “Simpler” e “Standard”. Elas são selecionadas informando o argumento cov.str="simpler" ou cov.str="standard" da função fit.geomodel. O comportamento padrão é adotar a estrutura “simpler” quando possível.

Simpler

A estrutura “simpler” exige que os dados sejam co-locados, i.e., todas as variáveis do modelo estão presentes em todos os pontos amostrais, e é baseada no trabalho de Ribeiro (2022). A principal característica dessa estrutura de covariância é que não é preciso especificar parâmetros de covariância cruzada (entre variáveis) no modelo multivariado. Em troca disso, a covariância cruzada é construída a partir das covariâncias marginais, mas “ligadas” pelo parâmetro de correlação entre as variáveis.

Por isso o objeto GeoModelformado retornará uma matriz de correlação quando essa estrutura for utilizada.


minv <- fit.geomodel(InvObj = inv, var_names = c('va', 'h'))
#> ---------------------------------------------
#> Ajustado utilizando máxima verossimilhança.
#> Use ... (control) para passar argumentos adicionais a optim().
#> ATENÇÁO! O ajuste pode levar alguns minutos!
#> ---------------------------------------------
#> Estrutura de Covariância adotada: simpler
#> Ajuste em escala irrestrita (log/atanh conforme o caso).
#> ---------------------------------------------
#> Ajustando...
#> ---------------------------------------------
#> Fim da maximização numérica.
#> ---------------------------------------------
#> Tempo de otimização: 0.65 segundos
#> ---------------------------------------------

minv
#> --------------------------------------
#>            Modelo ajustado            
#> --------------------------------------
#> Estrutura de Covariância: Simpler (Dados co-locados)
#> --------------------------------------
#> Parâmetros marginais:
#>          mu   sigmas     phis   taus
#> va 130.7685 630.7728  60.7584 0.0602
#> h   24.4500   0.5443 314.1510 0.5624
#> --------------------------------------
#> Matriz de correlação:
#>           va         h
#> va 1.0000000 0.7068323
#> h  0.7068323 1.0000000
#> --------------------------------------
#> Ajuste realizado na escala irrestrita (log/atanh) dos parâmetros.
#> --------------------------------------
#> Log-verossimilhança maximizada: -262.4712

Standard

A segunda estrutura de covariância é chamada “standard”, e constrói as covariâncias cruzadas por meio da declaração direta dos parâmetros no modelo. No caso multivariado as covariâncias são expressas aos pares de variáveis (um modelo com três variáveis terá três pares de covariâncias cruzadas).


minv <- fit.geomodel(InvObj = inv, var_names = c('va', 'h', 'd'),
                     cov.str = 'standard')
#> ---------------------------------------------
#> Ajustado utilizando máxima verossimilhança.
#> Use ... (control) para passar argumentos adicionais a optim().
#> ATENÇÁO! O ajuste pode levar alguns minutos!
#> ---------------------------------------------
#> Estrutura de Covariância adotada: standard
#> Ajuste em escala irrestrita (log/atanh conforme o caso).
#> ---------------------------------------------
#> Ajustando...
#> ---------------------------------------------
#> Fim da maximização numérica.
#> ---------------------------------------------
#> Tempo de otimização: 4.82 segundos
#> ---------------------------------------------

minv
#> --------------------------------------
#>            Modelo ajustado            
#> --------------------------------------
#> Estrutura de Covariância: Standard (Covariâncias cruzadas explícitas)
#> --------------------------------------
#> Parâmetros marginais:
#>          mu   sigmas        phis   taus
#> va 132.0463 637.5457      0.0031 0.1034
#> h   24.5335   0.0000 203422.4204 0.0000
#> d   29.8927   1.7966    161.0996 0.0917
#> --------------------------------------
#> Parâmetros cruzados:
#>        sigmas_c    phis_c
#> va X h   0.0000 7553.2910
#> va X d   0.0000    0.0004
#> h X d    1.1702  185.2058
#> --------------------------------------
#> Ajuste realizado na escala irrestrita (log/atanh) dos parâmetros.
#> --------------------------------------
#> Log-verossimilhança maximizada: -231.0795

O argumento crossed= recebe um lógico TRUE/FALSE, e regula se o modelo multivariado deve conter componente cruzado (covariância entre variáveis). Se crossed=FALSE, então um modelo multivariado será equivalente a ajustar cada variável de forma independente. O padrão é crossed=TRUE.

Além de especificar diretamente as covariâncias cruzadas, a estrutura “standard” também permite modificar ou mesclar efeitos cruzados e marginais. O argumento acc= da função fit.geomodel() recebe um valor lógico TRUE/FALSE, que determina se os efeitos cruzados devem ser espelhados no bloco de covariâncias marginais. O padrão é acc=TRUE.

O argumento common= também recebe TRUE/FALSE, e regula se deve ser incluído um efeito espacial adicional, comum e compartilhado a todas as variáveis. Se common=TRUE, então os parâmetros desse efeito espacial são passados em sigma0= e phi0=. O padrão é common=FALSE.

minv <- fit.geomodel(InvObj = inv, var_names = c('va', 'h', 'd'),
                     cov.str = 'standard',
                     common = TRUE)
#> ---------------------------------------------
#> Ajustado utilizando máxima verossimilhança.
#> Use ... (control) para passar argumentos adicionais a optim().
#> ATENÇÁO! O ajuste pode levar alguns minutos!
#> ---------------------------------------------
#> Estrutura de Covariância adotada: standard
#> Ajuste em escala irrestrita (log/atanh conforme o caso).
#> ---------------------------------------------
#> Ajustando...
#> ---------------------------------------------
#> Fim da maximização numérica.
#> ---------------------------------------------
#> Tempo de otimização: 9.38 segundos
#> ---------------------------------------------
minv
#> --------------------------------------
#>            Modelo ajustado            
#> --------------------------------------
#> Estrutura de Covariância: Standard (Covariâncias cruzadas explícitas)
#> --------------------------------------
#> Parâmetros marginais:
#>          mu   sigmas         phis   taus
#> va 132.0583 600.0380 3.500000e-03 0.1031
#> h   24.5339   0.0000 1.101179e+09 0.0000
#> d   29.8954   1.8826 1.541367e+02 0.0063
#> --------------------------------------
#> Parâmetros cruzados:
#>        sigmas_c       phis_c
#> va X h        0 1.325681e+08
#> va X d        0 0.000000e+00
#> h X d         0 1.973000e-01
#> --------------------------------------
#> Parâmetros do processo comum:
#>   sigma0     phi0
#> 1 1.1703 185.2404
#> --------------------------------------
#> Ajuste realizado na escala irrestrita (log/atanh) dos parâmetros.
#> --------------------------------------
#> Log-verossimilhança maximizada: -229.6847

Note que quanto maior a complexidade do modelo, mais difícil será o ajuste. Além do mais, é oportuno prezar pela parcimônia, pois modelos mais complexos tendem a trazer um ganho marginal. Uma maior fundamentação teórica da estrutura “standard” é encontrada em Orso (2024).

2.1.1.2 Função de autocorrelação

Outra definição exigida pelo modelo é o da função de autocorrelação utilizada. As opções atualmente disponíveis são Exponencial (“exponential”), Esférica (“spherical”) e Gaussiana (“gaussian”). Esse comando é passado ao argumento model= da função fit.geomodel().

No caso do ajuste multivariado, a mesma função de autocorrelação deve ser utilizada para todas as variáveis.


inv_gauss <- fit.geomodel(inv, c('va', 'h'),
                          model = 'spherical')
#> ---------------------------------------------
#> Ajustado utilizando máxima verossimilhança.
#> Use ... (control) para passar argumentos adicionais a optim().
#> ATENÇÁO! O ajuste pode levar alguns minutos!
#> ---------------------------------------------
#> Estrutura de Covariância adotada: simpler
#> Ajuste em escala irrestrita (log/atanh conforme o caso).
#> ---------------------------------------------
#> Ajustando...
#> ---------------------------------------------
#> Fim da maximização numérica.
#> ---------------------------------------------
#> Tempo de otimização: 0.62 segundos
#> ---------------------------------------------
inv_gauss
#> --------------------------------------
#>            Modelo ajustado            
#> --------------------------------------
#> Estrutura de Covariância: Simpler (Dados co-locados)
#> --------------------------------------
#> Parâmetros marginais:
#>          mu   sigmas   phis   taus
#> va 132.0759 637.5555 1.7658 0.1011
#> h   24.5707   0.7050 1.4966 0.4335
#> --------------------------------------
#> Matriz de correlação:
#>           va         h
#> va 1.0000000 0.7166856
#> h  0.7166856 1.0000000
#> --------------------------------------
#> Ajuste realizado na escala irrestrita (log/atanh) dos parâmetros.
#> --------------------------------------
#> Log-verossimilhança maximizada: -265.4749

inv_exp <- fit.geomodel(inv,  c('va', 'd'),
                        model = 'exponential')
#> ---------------------------------------------
#> Ajustado utilizando máxima verossimilhança.
#> Use ... (control) para passar argumentos adicionais a optim().
#> ATENÇÁO! O ajuste pode levar alguns minutos!
#> ---------------------------------------------
#> Estrutura de Covariância adotada: simpler
#> Ajuste em escala irrestrita (log/atanh conforme o caso).
#> ---------------------------------------------
#> Ajustando...
#> ---------------------------------------------
#> Fim da maximização numérica.
#> ---------------------------------------------
#> Tempo de otimização: 0.76 segundos
#> ---------------------------------------------
inv_exp
#> --------------------------------------
#>            Modelo ajustado            
#> --------------------------------------
#> Estrutura de Covariância: Simpler (Dados co-locados)
#> --------------------------------------
#> Parâmetros marginais:
#>          mu   sigmas     phis   taus
#> va 131.1646 630.7286  65.1582 0.0644
#> d   29.8774   5.6083 130.9550 0.0005
#> --------------------------------------
#> Matriz de correlação:
#>           va         d
#> va 1.0000000 0.6712474
#> d  0.6712474 1.0000000
#> --------------------------------------
#> Ajuste realizado na escala irrestrita (log/atanh) dos parâmetros.
#> --------------------------------------
#> Log-verossimilhança maximizada: -302.3471

As funções de autocorrelação podem ser visualizadas para cada variável ao se construir os semivariogramas empíricos, via emp_variogram()

variog_d <- emp_variogram(inv, var = 'd')

plot(variog_d)

Já o modelo ajustado via mínimos quadrados ponderados é obtido por meio de fit_variogram().


fit_variog_expo <- fit_variogram(emp = variog_d,
                              model = 'exponential')

fit_variog_spher <- fit_variogram(emp = variog_d,
                                  model = 'spherical')

plot(variog_d)
lines(fit_variog_expo, col = 'firebrick')
lines(fit_variog_spher, col = 'steelblue')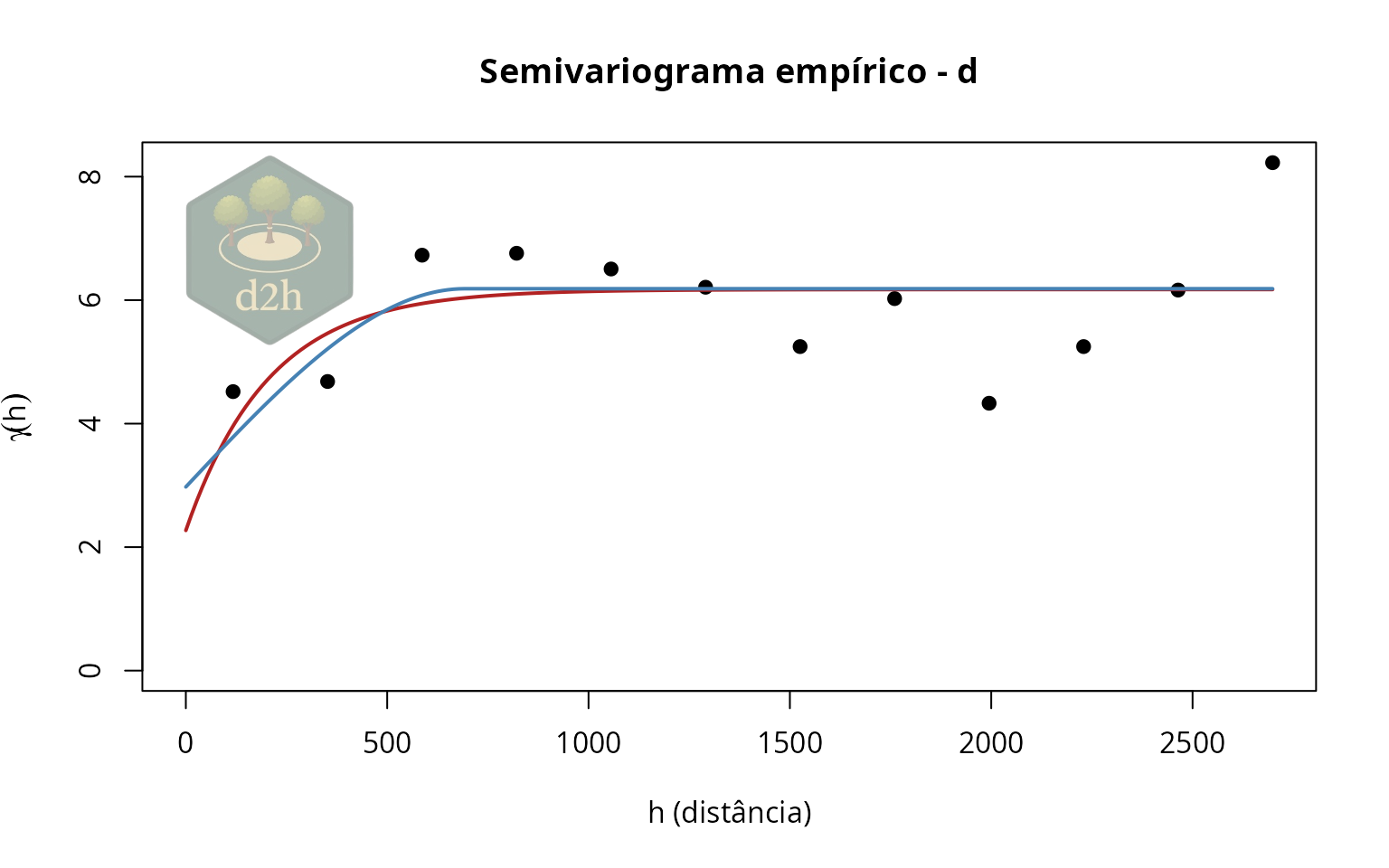

Os objetos obtidos via emp_variogram() e fit_variogram() não são estruturados, porém contém todas as informações relacionadas ao ajuste. Um variograma ajustado conterá os coeficientes ($coef), as informações agrupadas do semivariograma empírico ($emp), o modelo ($model) e o tipo de peso utilizado ($weights).

fit_variog_expo
#> $emp
#>                    bin npairs      dist    gamma
#> 1              [0,235]     40  117.3363 4.518429
#> 2            (235,469]    161  352.0088 4.682162
#> 3            (469,704]    175  586.6814 6.727993
#> 4            (704,939]    166  821.3539 6.759163
#> 5       (939,1.17e+03]    125 1056.0265 6.504407
#> 6  (1.17e+03,1.41e+03]    116 1290.6990 6.208984
#> 7  (1.41e+03,1.64e+03]     97 1525.3716 5.247692
#> 8  (1.64e+03,1.88e+03]     51 1760.0441 6.024429
#> 9  (1.88e+03,2.11e+03]     41 1994.7167 4.330022
#> 10 (2.11e+03,2.35e+03]     35 2229.3892 5.247650
#> 11 (2.35e+03,2.58e+03]     22 2464.0618 6.162764
#> 12 (2.58e+03,2.82e+03]      6 2698.7343 8.226217
#> 
#> $model
#> [1] "exponential"
#> 
#> $coef
#>     nugget      psill      range 
#>   2.270344   3.901815 206.389610 
#> 
#> $value
#> [1] 0.5644312
#> 
#> $weights
#> [1] "npairs"
#> 
#> attr(,"class")
#> [1] "d2h_variogram_fit"

2.1.1.3 Demais definições

Alguns parâmetros de fit.geomodel() auxiliam no ajuste e na apresentação de resultados. O primeiro é hmax=, que recebe um valor numérico e representa o limiar de distância para considerar independência espacial. A partir dessa distância, qualquer valor de covariância será definido como 0 (independência).

O argumento threshold= funciona de forma similar, mas em termos de correlação. O argumento recebe um valor numérico que representa a correlação mínima a ser considerada. Valores abaixo desse limiar serão definidos como 0. Veja que, como as funções de autocorrelação possuem 0 apenas como assíntota, então mesmo grandes distâncias terão um valor não nulo para correlação. Esse parâmetro funciona como um ponto de corte para definir manualmente o valor 0. Como consequência, os cálculos matriciais se tornam mais rápidos.

Um terceiro argumento é verbose=, que não tem efeito no ajuste, mas controla a quantidade de informações printadas no console durante o ajuste.

2.1.2 Valores iniciais dos parâmetros

A função fit.geomodel() pode receber sementes dos parâmetros para ajuste do modelo. Embora não seja obrigatório, o uso de sementes pode ser fator decisivo para a obtenção de ajustes satisfatórios e condizentes, pois modelos com muitos parâmetros frequentemente caem em ótimos locais onde a interpretação dos parâmetros fica prejudicada. Os argumentos dos parâmetros são sigmas=, sigmas_c=, phis=, phis_c=, mus=, taus=, sigma0= e phi0=.

sigmas=, sigmas_c e sigma0 são os parâmetros de covariância marginal (das variáveis), covariância cruzada e covariância do efeito comum, respectivamente. phis=, phis_c e phi0 são parâmetros de alcance marginal, alcance cruzada e alcance do efeito comum, respectivamente. Veja que se for adotada estrutura “Simpler” de covariância, apenas sigmas= é utilizado, pois as covariâncias cruzadas são obtidas indiretamente. Esses são os parâmetros interpretados como partial sill ou patamar.

mus= são os parâmetros de média das variáveis, e taus= são as variâncias não estruturadas, ou erro aleatório. No jargão da área, taus= são os nuggets ou efeito pepita.

Com exceção de sigma0 e phi0, todos os demais argumentos podem receber um vetor com mais de um valor, a depender do número de variáveis do modelo multivariado. Os argumentos sigmas=, phis=, mus= e taus= recebem vetores de mesmo tamanho que número de variáveis, ou seja, se são três variáveis, então sigmas = c(10, 20, 30) por exemplo.

Já os parâmetros cruzados recebem o mesmo número de parâmetros que os possíveis pares de variáveis, ou p*(p-1)/2 parâmetros, onde p é o número de variáveis. A ordem de passagem dos parâmetros importa, e segue a mesma sequência de variáveis informadas em var_names=.

Por exemplo, se var_names = c('Var1', 'Var2', 'Var3', 'Var4'), e se [1,2] é o parâmetro referente ao par Var1|Var2, então a ordem será c([1,2], [1,3], [1,4], [2,3], [2,4], [3,4]).


minv_semsementes <- fit.geomodel(InvObj = inv,
                                 var_names = c('va', 'd'),
                                 cov.str = 'standard'
                                 )
#> ---------------------------------------------
#> Ajustado utilizando máxima verossimilhança.
#> Use ... (control) para passar argumentos adicionais a optim().
#> ATENÇÁO! O ajuste pode levar alguns minutos!
#> ---------------------------------------------
#> Estrutura de Covariância adotada: standard
#> Ajuste em escala irrestrita (log/atanh conforme o caso).
#> ---------------------------------------------
#> Ajustando...
#> ---------------------------------------------
#> Fim da maximização numérica.
#> ---------------------------------------------
#> Tempo de otimização: 1.21 segundos
#> ---------------------------------------------
minv_semsementes
#> --------------------------------------
#>            Modelo ajustado            
#> --------------------------------------
#> Estrutura de Covariância: Standard (Covariâncias cruzadas explícitas)
#> --------------------------------------
#> Parâmetros marginais:
#>          mu   sigmas   phis   taus
#> va 131.9934 558.3727 0.0020 0.1040
#> d   29.8942   0.0000 2.7398 0.0001
#> --------------------------------------
#> Parâmetros cruzados:
#>        sigmas_c  phis_c
#> va X d   5.9674 169.085
#> --------------------------------------
#> Ajuste realizado na escala irrestrita (log/atanh) dos parâmetros.
#> --------------------------------------
#> Log-verossimilhança maximizada: -230.705


minv_comsementes <- fit.geomodel(InvObj = inv,
                                 var_names = c('va', 'd'),
                                 cov.str = 'standard',
                                 sigmas = c(300, 2),  # Volume tem mais variabilidade
                                 phis = c(150, 200),
                                 taus = c(300, 3)
                                 )
#> ---------------------------------------------
#> Ajustado utilizando máxima verossimilhança.
#> Use ... (control) para passar argumentos adicionais a optim().
#> ATENÇÁO! O ajuste pode levar alguns minutos!
#> ---------------------------------------------
#> Estrutura de Covariância adotada: standard
#> Ajuste em escala irrestrita (log/atanh conforme o caso).
#> ---------------------------------------------
#> Ajustando...
#> ---------------------------------------------
#> Fim da maximização numérica.
#> ---------------------------------------------
#> Tempo de otimização: 1.22 segundos
#> ---------------------------------------------
minv_comsementes
#> --------------------------------------
#>            Modelo ajustado            
#> --------------------------------------
#> Estrutura de Covariância: Standard (Covariâncias cruzadas explícitas)
#> --------------------------------------
#> Parâmetros marginais:
#>          mu   sigmas    phis   taus
#> va 131.8451 555.7968 71.2316 1.3717
#> d   29.8950   0.0000 12.8767 0.0000
#> --------------------------------------
#> Parâmetros cruzados:
#>        sigmas_c  phis_c
#> va X d   5.9671 169.054
#> --------------------------------------
#> Ajuste realizado na escala irrestrita (log/atanh) dos parâmetros.
#> --------------------------------------
#> Log-verossimilhança maximizada: -230.292

A passagem de sementes dos parâmetros é opcional, mas se informada, o vetor de parâmetros deve ter a quantidade correta de elementos. Não há obrigatoriedade de se passar todos os argumentos. Por exemplo, utilizar sigmas= não torna obrigatório utilizar sigmas_c= etc.

Uma boa prática é fazer uso dos valores obtidos com fit_variogram() de cada variável como sementes para ajuste do modelo. Veja que, embora seja comum o ajuste de modelos a partir do semivariograma, o pacote {d2h} realiza o ajuste via máxima verossimilhança.

O argumento irr= recebe um valor lógico TRUE/FALSE (o padrão é TRUE), que indica se os parâmetros serão ajustados na escala original (restrita, irr=FALSE), ou se serão ajustados em uma escala transformada (irrestrita, irr=TRUE). Escala restrita significa que os parâmetros possuem um suporte limitado, por exemplo variâncias são sempre positivas e correlação sempre entre 0 e 1, portanto o algoritmo deverá respeitar esses limites.

Já o ajuste em escala irrestrita envolve a transformação log() para parâmetros de variância/covariância, e transformação atanh() para os parâmetros de correlação. Dessa forma, os parâmetros transformados podem assumir qualquer valor real durante a maximização, o que diminui as chances de matriz não PD ou valores muito pŕoximos do limite do suporte dos parâmetros.

2.2 Predição (krigagem)

2.2.1 Definições da Krigagem

Após ajuste do modelo, esse pode ser utilizado para estimar novos pontos com a função predict(). A documentação pode ser consultada via ?predict.geomodel ou ?predict,GeoModel-method. Os principais argumentos são

object=, que recebe o modelo ajustado da classe GeoModel;
newdata=, que recebe um objeto da classe sf contendo novos pontos para estimativa;
intervals=, que recebe um valor lógico TRUE/FALSE informando se os intervalos de confiança devem ser estimados.


# Criando novos pontos
newd <- sf::st_sfc(sf::st_point(c(564012, 8205847)),
                   sf::st_point(c(563905, 8206187)),
                   crs = 32721) |> sf::st_as_sf()

preds <- predict(object = inv_exp, # Objeto ajustado, da classe `GeoModel`.
                 newdata = newd,   # Novos dados para estimativa, classe `sf`.
                 intervals = TRUE) # TRUE para criar intervalos de confiança.
#> Predição para novos pontos...

preds
#> $mu
#> $mu$va
#> [1]  91.69248 139.44858
#> 
#> $mu$d
#> [1] 24.80265 30.24794
#> 
#> 
#> $var
#> $var$va
#> [1]  42.58447 616.73904
#> 
#> $var$d
#> [1] 0.2025546 4.4600110
#> 
#> 
#> $n_nd
#> [1] 2
#> 
#> $intervals
#> $intervals$va
#>         LI       LS
#> 1 78.90239 104.4826
#> 2 90.77438 188.1228
#> 
#> $intervals$d
#>         LI       LS
#> 3 23.92054 25.68475
#> 4 26.10875 34.38714

Por padrão a função retorna uma lista contendo quatro elementos:

$mu, contendo as médias estimadas em cada ponto para cada variável
#var, contendo as variâncias estimadas de cada ponto para cada variável
$n_nd, um inteiro contendo o número de pontos estimados.
$intervals, uma lista contendo dataframes de cada variável com limites superiores e inferiores do intervalo de predição.

Além dos argumentos principais, predict() função também recebe os demais argumentos:

nugget=, que recebe TRUE/FALSE para incluir efeito pepita na predição. Padrão é TRUE;
krig.type=, caractere que recebe "ordinary" ou "universal" para o tipo de krigagem. Padrão é "ordinary";
fast=, lógico TRUE/FALSE que regula o uso de cálculo otimizado das matrizes de covariância;
confirm=, lógico TRUE/FALSE que regula o pedido de confirmação de predição para muitos pontos. Se TRUE, será necessário confirmar a predição após excever confirm_threshold=;
confirm_threshold=, inteiro informando o número máximo de novos pontos antes de solicitar confirmação de predição;
conf=, numérico entre 0 e 1 com o nível de confiança. O padrão é 0.95.
distref=, caractere entre "centroid" e "edge" regulando o ponto inicial para cálculo das distâncias espaciais. Só relevante se newdata= recebe polígonos. O padrão é 'centroid'.

2.2.2 Área de densidade de predição

Embora disponível, predict() foi construída para ser usada internamente no pacote {d2h}, pois um dos principais produtos de modelos geoestatísticos é o mapa de predição. Isso envolve a criação de um grid sistemático de novos pontos, que irão recobrir a área de interesse e com isso estimar as variáveis relevantes.

A criação desse grid pode ser trabalhosa, por isso o pacote {d2h} cria esse grid automaticamente a partir dos pontos amostrados, e realiza a predição. Tal recurso é disponibilizado via a função krig().

Os principais argumentos da função são:

object=, um objeto de modelo ajustado da classe GeoModel;
cellsize=, que pode ser um número (50) ou um vetor bidimensional c(50, 60) que informa o tamanho do grid de predição. Se for um número, será uma malha quadrada. Se bidimensional, será interpretado na forma c("X", "Y").

cellsize= se refere ao tamanho da célula de predição, em metros. Portanto cellsize=50 quer dizer que a predição será feita em uma malha com pontos espaçados a cada 50 metros. Se o número de pontos gerados por esse grid for superior ao limite confirm_threshold= da função predict(), então será solicitada uma confirmação de predição.

Veja que o número de pontos é proporcional ao tamanho da célula e à área de amostragem. Portanto diferentes conjuntos de dados terão diferentes resoluções espaciais.


kinv <- krig(object = inv_exp, # Objeto de ajusta da classe `GeoModel`
             cellsize = 30     # Número ou vetor bidimensional com a resolução espacial
             )
#> `InvObj` de referência não possui bordadura.
#> Será criada uma envoltória convexa.
#> Predição para novos pontos...
#> -------------------------------------------
#> SRC dos pontos gerados: WGS 84 / UTM zone 21S [EPSG: 32721]
#> -------------------------------------------
#> Estimados 2376 pontos em 0.20 secs
#> -------------------------------------------

kinv
#> --------------------------------------
#>         Krigagem espacial (d2h)       
#> --------------------------------------
#> Classe: GeoModelKrig
#> Tipo de krigagem: ordinary 
#> Variáveis preditas: va, d 
#> Cellsize (m): 30 | Nugget: incluído | C++ (fast): sim 
#> --------------------------------------
#> Área delimitada a partir de envoltória convexa.
#> CRS do grid de predição: WGS 84 / UTM zone 21S 
#> Número de pontos no grid de predição: 2376 
#> Área de predição ~2135534 m² (213.55 ha)
#> Tempo de krigagem: 0.2 secs 
#> --------------------------------------
#> Estatísticas médias das predições (por variável):
#>  variavel    n    Media Variancia     Min      Max
#>        va 2376 131.8566  565.7622 89.3020 174.1825
#>         d 2376  30.0267    4.1228 24.4294  34.5034

Por padrão, a função cria uma envoltória convexa no entorno dos pontos amostrados. A malha de predição é recortada nessa envoltória.


plot(kinv)

No entanto, se algum polígono for passado para o argumento newarea=, então a malha de predição será feita com base nesse polígono.


# caminho até arquivo
caminho_ate_borda <- system.file('extdata',  'bordas.shp',  package = 'd2h')

# Carregando shapefile com o pacote `{sf}`.
borda <- sf::st_read(caminho_ate_borda)
#> Reading layer `bordas' from data source 
#>   `/tmp/RtmpaxaI0n/temp_libpath4be22a841e79/d2h/extdata/bordas.shp' 
#>   using driver `ESRI Shapefile'
#> Simple feature collection with 1 feature and 1 field
#> Geometry type: POLYGON
#> Dimension:     XY
#> Bounding box:  xmin: 563598.9 ymin: 8205658 xmax: 566424.9 ymax: 8207792
#> Projected CRS: WGS 84 / UTM zone 21S

kinv <- krig(object = inv_exp,
             cellsize = 30,
             newarea = borda   # `newarea=` deve receber um objeto da classe `sf`.
             )
#> Realizando predição a partir de `newarea`.
#> Predição para novos pontos...
#> -------------------------------------------
#> SRC dos pontos gerados: WGS 84 / UTM zone 21S [EPSG: 32721]
#> -------------------------------------------
#> Estimados 2470 pontos em 0.16 secs
#> -------------------------------------------


plot(kinv)

Além disso, se o objeto Inv já possui um objeto espacial de bordadura (informado via método talhao(), veja o guia introdutório), então essa bordadura será utilizada para delimitar a área de predição.

inv2 <- talhao(inv, source = caminho_ate_borda, recalc = TRUE)
#> Objeto espacial de talhão incluído no inventário

minv2 <- fit.geomodel(inv2,  c('va',  'd'))
#> ---------------------------------------------
#> Ajustado utilizando máxima verossimilhança.
#> Use ... (control) para passar argumentos adicionais a optim().
#> ATENÇÁO! O ajuste pode levar alguns minutos!
#> ---------------------------------------------
#> Estrutura de Covariância adotada: simpler
#> Ajuste em escala irrestrita (log/atanh conforme o caso).
#> ---------------------------------------------
#> Ajustando...
#> ---------------------------------------------
#> Fim da maximização numérica.
#> ---------------------------------------------
#> Tempo de otimização: 0.97 segundos
#> ---------------------------------------------

kinv2 <- krig(minv2, cellsize = 30)
#> Predição para novos pontos...
#> -------------------------------------------
#> SRC dos pontos gerados: WGS 84 / UTM zone 21S [EPSG: 32721]
#> -------------------------------------------
#> Estimados 2470 pontos em 0.15 secs
#> -------------------------------------------

plot(kinv2)

A função krig() recebe também os argumentos crs_grid= e buffer=:

crs_grid= recebe um número contendo o código EPSG do SRC desejado para o grid. O padrão é uma projeção UTM, mas outra opção pode ser útil se o grid ocupar mais de um fuso, por exemplo.
buffer= recebe um número que representa um buffer de predição, em metros, no entorno da área de predição. O padrão é 5 metros.

Além disso, os demais argumentos ... de krig() serão repassados para a função predict(), portanto krig() também recebe os demais argumentos de predict().

A função krig() retorna um novo objeto de classe GeoModelKrig, herdeira da classe GeoModel. Um método possível para GeoModelKrig é o método plot(). Por isso, objetos gerados com krig() podem ser plotados seguindo alguns argumentos específicos do método. A documentação pode ser acessada via ?plot.krig ou ?plot,GeoModelKrig-method.

Por padrão, plot(GeoModelKrig) irá retornar um mapa de krigagem da estimativa da média da primeira variável do modelo. O uso de outros argumentos altera propriedades da plotagem.

Os principais argumentos para plotar um GeoModelKrig são:

x=, um objeto retornado da krigagem, de classe GeoModelKrig;
variavel=, caractere contendo o nome da variável espacializada. Por padrão é a primeira variável do modelo;
measure=, um caractere podendo ser "mean", "variance", "LI" ou "LS". Que se referem à espacialização da média, variância, Limite Inferior e Limite Superior, respectivamente, do intervalo de confiança;
add_contour=, lógico TRUE/FALSE indicando se curvas de níveis devem ser adicionadas.


plot(kinv,
     variavel = 'd',        # Poderia ser "va" ou "d", dado meu conjunto de dados
     measure = 'variance',  # Será feita espacialização da variância;
     add_contour = TRUE,    # Adiciona curvas de nível
     nlevel_contour = 5     # Adiciona 5 curvas de nível
     )

Além desses argumentos, outros argumentos que controlam a forma e distribuição das curvas de nível, bem como a paleta de cores da predição, podem ser consultadas em ?plot.krig ou ?plot,GeoModelKrig-method.

Tal qual a plotagem do objeto Inv, a função plot() também recebe outros argumentos genéricos da função de plotagem do R base.

3. Opções de conversão e salvamento

A malha de novos pontos estimados por krig() pode ser facilmente convertida para vetor ou raster com os métodos to.vector() e to.raster(), respectivamente.

O método to.vector() converte o GeoModelKrig para vetor. O tipo de vetor resultante é controlado por type=, que pode ser “point” ou “polygon”. Se type="point", então será gerado um vetor de pontos. Se type="polygon", serão geradas feições poligonais, com dimensão igual àquela especificada em cellsize= da função krig().

Também é possível definir o sistema de coordenadas de saída, informando o código EPSG no argumento out_crs=. O padrão é o mesmo sistema de coordenadas dos dados de entrada.

A tabela de atributos do objeto espacial gerado contém todas as informações de estimativa. Para mais informações sobre to.vector() consulte a documentação com ?to.vector.

vetor <- to.vector(x =  kinv,       # x recebe o objeto `GeoModelKrig`
                   type = 'point',  # type pode ser "point" ou "polygon"
                   out_crs = 4326)  # Será gerado shapefile no sistema geográfico WGS 84

# Gera um objeto da classe `sf`
class(vetor)
#> [1] "sf"         "data.frame"

Já o método to.raster() converte a malha de pontos em um raster com a mesma resolução definida em cellsize=, isto é, cellsize= regula a resolução do raster gerado.

Diferentemente do vetor, é preciso escolher a variável que será espacializada, bem como a medida (média, variância, LI ou LS).

Por fim, o argumento mask_bounds= recebe um lógico TRUE/FALSE que regula se o raster deve receber uma máscara fora dos pixels de predição. O padrão é TRUE. Para mais informações sobre to.raster() consulte a documentação com ?to.raster.


img <- to.raster(x = kinv,           # x recebe o objeto `GeoModelKrig`
                 variavel = 'va',    # variavel recebe o nome de uma das variáveis modeladas
                 measure = 'mean',   # measure recebe caractere da medida
                 mask_bounds = TRUE  # mask_bounds regula se uma máscara deve ser adicionada
                 )

# Gera objeto da classe `SpatRaster` do pacote `{terra}`
class(img)
#> [1] "SpatRaster"
#> attr(,"package")
#> [1] "terra"

A malha estimada via krig() pode ser salva de três formas:

Em formato csv (.csv)
Em formato shapefile (.shp)
Em formato raster (.tiff)

O método utilizado para salvar é salvar(), com os argumentos:

x=, o objeto GeoModelKrig resultante de krig(). Obrigatório;
nome=, caractere opcional com nome do arquivo. Se não fornecido, um nome genérico será fornecido. A extensão do arquivo pode ser fornecida aqui.
formato=, um caractere contendo “csv”, “shp”, etc.. Pode ser omitido se o formato ser informado em nome=.

Para o salvamento em csv, será gerado um arquivo de texto contendo as informações dos IDs/Parcelas, caso tenham sido fornecidos em Inv. Predições de média, variância e limites de confiança caso intervals=TRUE em krig(). Além das coordenadas dos novos pontos da malha de predição.

Para o salvamento em shapefile (shp), a mesma informação do csv será inserida em pontos espacializados utilizando as mesmas coordenadas. Os argumentos de to.vector() também podem ser passados para modificar o vetor exportado.

Para o salvamento em tiff, são aceitos formatos “tif”, “tiff”, “geotiff” ou “raster”. Tal opção irá gerar um raster cuja resolução segue o informado em cellsize= da função krig(). A malha de predição será transformada em uma imagem cujos pontos estarão no centro dos pixels. Veja que, por consequência, cellsize= representa a resolução de saída do raster gerado. Os argumentos de to.raster() também podem ser utilizados para modificar o raster de saída.


# Para CSV
salvar(kinv, nome = 'resultados', formato = 'csv')
salvar(kinv, nome = 'resultados.csv')   # Equivalente


# Para shapefile
salvar(kinv, nome = 'resultados_shapes.shp')
salvar(kinv, nome = 'resultados_shapes', formato = 'shp')  # Equivalente

salvar(kinv, nome = 'resultados_shapes.shp',
       type = 'polygon',  # Os argumentos de to.vector() podem ser utilizados
       out_crs = 4326)    # Os argumentos de to.vector() podem ser utilizados



# Para raster
salvar(kinv, nome = 'results_raster.tif')
salvar(kinv, nome = 'results_raster', formato = 'tif')  # Equivalente

salvar(kinv, nome = 'results_raster.tif',
       measure = 'variance')  # Os argumentos de to.raster() podem ser utilizados

1. Carregando um objeto Inv